Vùng liên thông trong đồ thị là tập hợp các đỉnh mà từ một đỉnh bất kỳ có đường đi trực tiếp hoặc gián tiếp đến các đỉnh khác trong tập hợp đó. Cho đồ thị vô hướng có ~N~ đỉnh, ~M~ cạnh. Hãy liệt kê các vùng liên thông trong đồ thị. Trong mỗi vùng các đỉnh được sắp xếp thành dãy tăng. Mỗi vùng liên thông trên một hàng. Mỗi số cách nhau một dấu cách.

Dữ liệu vào gồm:

• Dòng 1: Ghi số nguyên ~N~ và ~M~ ~(M, N ≤ 3000)~.

• ~M~ dòng tiếp theo, mỗi dòng ghi số nguyên dương ~u~ và ~v~ thể hiện có đường đi giữa hai đỉnh ~u~ và ~v~ ~(u, v ≤ N)~.

Kết quả:

Gồm nhiều dòng là các vùng liên thông trong đồ thị. Trong mỗi vùng các đỉnh được sắp xếp thành dãy tăng. Mỗi số cách nhau một dấu cách, mỗi vùng liên thông trên một hàng.

Ví dụ

INPUT

12 7
1 2
2 5
2 6
6 10
3 4
9 11
9 12

OUTPUT

1 2 5 6 10
3 4
7
8
9 11 12

Tại quần đảo ZXY có N hòn đảo, một số hòn đảo đã có cầu nối với nhau. Từ đảo này ta có thể đi sang đảo khác bằng đường đi trực tiếp hoặc đi gián tiếp qua các đảo khác. Để thuận tiện cho các phương tiện đi lại, ban quản lý sẽ xây thêm một số cầu để từ một đảo ta có thể đi đến các đảo còn lại trong quần đảo. Hãy cho biết, ban quản lý cần xây ít nhất bao nhiêu cầu?

Dữ liệu vào:

• Dòng 1: Ghi số nguyên N và M (M, N ≤ 3000). • M dòng tiếp theo, mỗi dòng ghi số nguyên dương u và v thể hiện có đường đi giữa hai đỉnh u và v (u, v ≤ N).

Kết quả: Ghi ra số cầu ít nhất cần xây thêm.

Ví dụ: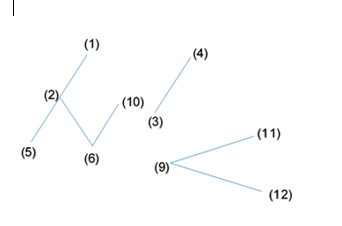

INPUT

12 7                                        
1 2
2 5
2 6
6 10
3 4
9 11
9 12

OUTPUT

4

Tại quần đảo ZXY có N hòn đảo, một số hòn đảo đã có cầu nối với nhau, không có chu trình. Từ đảo này ta có thể đi sang đảo khác bằng đường đi trực tiếp hoặc đi gián tiếp qua các đảo khác.

Jame vừa đến hòn đảo S, anh muốn đi bằng đường bộ đến các đảo khác. Khi đến một đảo, anh ấy có thể nghỉ ngơi ở đảo ấy hoặc đi tiếp sang các đảo khác. Tất nhiên, anh ấy chỉ muốn tham quan mỗi đảo một lần.

Hãy tìm số đảo nhiều nhất mà Jame có thể tham quan bằng đường bộ.

Dữ liệu vào gồm:

• Dòng 1: Ghi số nguyên dương N, M và S (M, N ≤ 3000, S ≤ N).
• M dòng tiếp theo, mỗi dòng ghi số nguyên dương u và v thể hiện có đường đi giữa hai đỉnh u và v (u, v ≤ N).

Kết quả: Ghi ra số đảo nhiều nhất mà Jame có thể tham quan bằng đường bộ.

Ví dụ:

INPUT

12 7 2
1 2
2 5
2 6
6 10
3 4
9 11
9 12

OUTPUT

3

(gồm các đảo 10 6 2)

Tại quần đảo ZXY có ~N~ hòn đảo, một số hòn đảo đã có cầu nối với nhau, không có chu trình. Từ đảo này ta có thể đi sang đảo khác bằng đường đi trực tiếp hoặc đi gián tiếp qua các đảo khác.

Jame vừa đến hòn đảo ~S~, anh muốn đi bằng đường bộ đến các đảo khác. Khi đến một đảo, anh ấy có thể nghỉ ngơi ở đảo ấy hoặc đi tiếp sang các đảo khác. Tất nhiên, anh ấy chỉ muốn tham quan mỗi đảo một lần. Do thời gian đi du lịch không nhiều, nên anh ấy muốn tham qua ~K~ đảo trong quần đảo ZXY.

Hãy tìm các hành trình mà Jame có thể tham quan bằng đường bộ theo yêu cầu trên.

Dữ liệu vào gồm:

• Dòng 1: Ghi số nguyên dương ~N, M, S~ và ~K~ ~(M, N ≤ 3000, K , S ≤ N)~.
• ~M~ dòng tiếp theo, mỗi dòng ghi số nguyên dương ~u~ và ~v~ thể hiện có đường đi giữa hai đỉnh ~u~ và ~v~ ~(u, v ≤ N)~.

Kết quả: Ghi ra các hành trình tham quan đi qua ~K~ hòn đảo. Mỗi số cách nhau một dấu cách. Nếu không có phương án tham quan, ghi ra ~-1~.

Ví dụ:

INPUT

12 7 1 3
1 2
2 5
2 6
6 10
3 4
9 11
9 12

OUTPUT

5 2 1
6 2 1

(truy vết ngược)

Vùng liên thông trong đồ thị là tập hợp các đỉnh mà từ một đỉnh bất kỳ có đường đi trực tiếp hoặc gián tiếp đến các đỉnh khác trong tập hợp đó. Cho đồ thị vô hướng có ~N~ đỉnh, ~M~ cạnh. Các đỉnh được đánh số từ ~1~ tới ~N~. Chi phí thăm đỉnh thứ ~i~ là ~t_i~. Hãy tìm các vùng liên thông có tổng chi phí nhỏ hơn hoặc bằng ~S~.

Dữ liệu vào gồm:

• Dòng 1: Ghi số nguyên dương ~N, M~ và ~S~ ~(M, N ≤ 3000, S ≤ 10^9)~.
• Dòng 2: Ghi ~N~ số nguyên dương ~t_i~ là chi phí thăm đỉnh ~i~ ~(t_i ≤ 10^9)~.
• ~M~ dòng tiếp theo, mỗi dòng ghi số nguyên dương ~u~ và ~v~ thể hiện có đường đi giữa hai đỉnh ~u~ và ~v~ ~(u, v ≤ N)~.

Kết quả: Ghi ra các vùng liên thông tìm được. Mỗi vùng liên thông ghi trên một hàng. Mỗi số cách nhau một dấu cách. Nếu không có ghi ra ~-1~.

Ví dụ:

INPUT

12 7 5
1 2 3 1 2 4 4 4 3 3 2 1
1 2
2 5
2 6
6 10
3 4
9 11
9 12

OUTPUT

3 4
7
8

Vùng liên thông trong đồ thị là tập hợp các đỉnh mà từ một đỉnh bất kỳ có đường đi trực tiếp hoặc gián tiếp đến các đỉnh khác trong tập hợp đó. Cho đồ thị vô hướng có ~N~ đỉnh, ~M~ cạnh. Các đỉnh được đánh số từ ~1~ tới ~N~. Chi phí thăm đỉnh thứ ~i~ là ~t_i~. Bạn có một vé miễn phí để dùng một lần khi thăm ~1~ đỉnh.

Bạn ghé thăm các đỉnh trong vùng liên thông có nhiều đỉnh nhất và sử dụng vé miễn phí để tổng chi phí nhỏ nhất.

*Dữ liệu vào: *

• Dòng 1: Ghi số nguyên dương ~N~, ~M~ ~(M, N ≤ 3000)~.
• Dòng 2: Ghi ~N~ số nguyên dương ~t_i~ là chi phí thăm đỉnh ~i~ (~t_i~ ≤ ~10^9~).
• ~M~ dòng tiếp theo, mỗi dòng ghi số nguyên dương ~u~ và ~v~ thể hiện có đường đi giữa hai đỉnh ~u~ và ~v~ ~(u, v ≤ N)~.

Kết quả: Ghi ra số đỉnh được thăm nhiều nhất và tổng chi phí nhỏ nhất tìm được.

Ví dụ:

INPUT

12 7
1 2 3 1 2 4 4 4 3 3 2 1
1 2
2 5
2 6
6 10
3 4
9 11
9 12

OUTPUT

5 8

(Chọn vùng nhiều đỉnh nhất: 1, 2, 5, 6, 10; Chi phí 1 + 2 + 2 + 4 + 3 = 12. Dùng vé miễn phí cho đỉnh 6, thu được tổng chi phí: 12-4=8)