Kì thi đại học đã rất gần rồi, với danh hiệu HSGQG, Kami chỉ cần qua được kì thi tốt nghiệp là có thể được nhận vào trường đại học mà cô hằng mơ ước. Điều đầu tiên cần làm của Kami lúc này là lấy lại gốc các môn tự nhiên, và thử thách đầu tiên chính là môn Hóa. Hãy cùng ôn tập với cô ấy nhé ^ ^.

Cho hỗn hợp 2 kim loại ~Fe, Mg~ tác dụng với ~Cl_2~ dư trong nhiệt độ cao, sau phản ứng thu được hỗn hợp 2 muối khan. Biết khối lượng của hỗn hợp trước và sau phản ứng, tìm khối lượng của từng kim loại ban đầu.

Cho ~Fe = 56, Mg = 24, Cl = 35.5~.

INPUT :

• Dòng đầu tiên chứa số nguyên dương ~T (T ≤ 10^6)~ là số lượng câu hỏi.

• ~T~ dòng tiếp theo mỗi dòng chứa 2 số ~N,M~ nguyên dương ~( N, M ≤ 10^5(gam) )~ là tổng khối lượng của 2 kim loại ban đầu và tổng khối lượng hỗn hợp sau phản ứng.

OUTPUT :

• Gồm ~T~ dòng, mỗi dòng chứa 2 số nguyên là khối lượng của từng kim loại ban đầu. Dữ liệu đảm bảo đáp án của các câu hỏi luôn là số nguyên.

Ví dụ:

Input 1

1
184 610

Output 1

112 72

Subtask 1: ~50~% số test thỏa mãn ~T ≤ 10^3~.

Subtask 2: ~50~% số test thỏa mãn ~T ≤ 10^6~.

Sau một tuần học ở lớp lập trình thi đấu, Aoi đã thành thục được các thao tác với mảng ~1~ chiều. Vì thế, trong buổi học hôm nay, em ấy sẽ được học về mảng ~2~ chiều. Bài tập của em lần này sẽ là in ra màn hình một mảng ~2~ chiều gồm toàn các số giống nhau. Rút kinh nghiệm về sự cố lần trước (đọc đề bài DIFF để biết thêm chi tiết), Aoi quyết định lần này sẽ chỉ in ra số 1 mà thôi, như thế thì sẽ khó có thể mà xuất hiện các số khác nhau được nữa. Thế nhưng, đời không như mơ, mảng ~2~ chiều em in ra lần này vẫn chứa các số khác nhau :'<. Tuy vậy lần này Aoi đã tiến bộ hơn lần trước khi code của em chỉ in ra số ~0~ hoặc ~1~. Sau khi quan sát các mảng ~2~ chiều mình in ra, cô bé phát hiện một tính chất thú vị, đó là sẽ có một số mảng con chỉ gồm toàn các số ~1~. Cô bé tò mò muốn biết liệu có bao nhiêu mảng con thỏa mãn đặc điểm này. Nhưng em ấy sớm nhận ra rằng, con số này sẽ có thể vô cùng lớn và việc đếm sẽ rất khó khăn. Vì thế, hãy giúp Aoi nhé.

Nhắc lại, xét mảng ~2~ chiều ~A~ gồm ~N~ hàng và ~M~ cột. Gọi ô ở hàng ~i~ và cột ~j~ là ô ~A_{ij}~. Một mảng con sẽ được xác định bằng ~4~ số nguyên dương ~x_1, y_1, x_2, y_2 (1 ≤ x_1 ≤ x_2 ≤ N, 1 ≤ y_1 ≤ y_2 ≤ M)~ và sẽ gồm các ô ~A_{ij}~ thỏa ~x_1 ≤ i ≤ x_2~ và ~y_1 ≤ j ≤ y_2~.

INPUT:

• Dòng đầu tiên gồm ~2~ số nguyên dương ~N, M~ lần lượt là số hàng và số cột.

• ~N~ dòng tiếp theo, mỗi dòng gồm ~M~ số nguyên có giá trị bằng ~0~ hoặc ~1~.

OUTPUT:

• Gồm ~1~ số nguyên không âm duy nhất là số lượng mảng con chỉ gồm các số ~1~.

VÍ DỤ

Input 1

3 3
0 1 0
1 1 0
1 1 1

Output 1

15

Input 2

5 5
0 0 0 0 0
0 1 1 1 0
0 1 1 1 0
0 1 1 1 0
0 0 0 0 0

Output 2

36

Giải thích ví dụ 1: https://drive.google.com/drive/folders/1q6V3CWdMjNmpHWymFF6KcYNVL6sE5hs_?usp=sharing

Subtask 1: ~20~% số test thỏa mãn ~N,M ≤ 10~.

Subtask 2: ~30~% số test thỏa mãn ~N,M ≤ 100~.

Subtask 3: ~20~% số test thỏa mãn ~N,M ≤ 500~.

Subtask 4: ~30~% số test thỏa mãn ~N,M ≤ 2000~.

C là người làm công tác khí tượng, đảm nhiệm vai trò đo lường nhiệt độ, áp suất không khí và nhiều thông số khác trên các đỉnh núi. Khu vực mà C được chuyển công tác tới lần này là một dãy núi gồm ~N~ ngọn núi liên tiếp nhau. C đánh số các ngọn núi theo thứ tự từ 1 tới ~N~ và ngọn núi thứ ~i~ có độ cao là ~h_i~. C đã lắp đặt ~N~ thiết bị đo lường trên ~N~ đỉnh núi, mỗi đỉnh núi 1 thiết bị. Để nhận dữ liệu từ các thiết bị này, C cần lắp đặt các thiết bị thu sóng. Tuy nhiên, nền kinh tế đang gặp nhiều khó khăn do đại dịch Covid-19 đã khiến ngân sách trở nên eo hẹp. Vì thế, C chỉ được cung cấp đủ kinh phí để chi trả cho việc lắp đặt đúng 2 thiết bị thu sóng mà thôi. Vì lý do kỹ thuật nên vùng quét của các thiết bị thu sóng không được giao nhau. Do đó, C quyết định chia dãy núi thành 2 nhóm, mỗi nhóm có ít nhất 1 ngọn núi. Nhóm đầu tiên gồm các ngọn núi được đánh số từ ~1~ tới ~K~, nhóm còn lại gồm các ngọn núi đánh số từ ~K + 1~ tới ~N~. Sau đó, C sẽ đặt một thiết bị thu sóng ở một trong các ngọn núi từ ~1~ tới ~K~ và nó sẽ được kết nối với tất cả các thiết bị đo lường trên các ngọn núi từ ~1~ tới ~K~. Thiết bị thu sóng còn lại sẽ được đặt ở một trong các ngọn núi từ ~K + 1~ tới ~N~ và được kết nối với các thiết bị đo lường còn lại. Lượng năng lượng cần thiết cho việc kết nối giữa 1 thiết bị thu sóng và 1 thiết bị đo lường sẽ bằng chênh lệch độ cao giữa vị trí lắp đặt của 2 thiết bị. Cụ thể hơn, lượng năng lượng cần thiết cho việc kết nối thiết bị đo lường ở đỉnh ~i~ và thiết bị thu sóng ở đỉnh ~j~ sẽ có giá trị là ~|h_i - h_j|~. C đương nhiên làm muốn tổng lượng năng lượng cần thiết để kết nối tất cả các thiết bị với nhau là bé nhất. Tuy nhiên, có tới ~N - 1~ cách chia dãy núi thành 2 nhóm, và với mỗi cách lại có rất nhiều vị trí đặt thiết bị thu sóng khác nhau. Vì thế, với các thông tin về dãy núi mà C cung cấp, bạn hãy giúp anh ấy chọn phương án mà tổng năng lượng cần thiết là nhỏ nhất nhé.

INPUT

• Dòng đầu tiên là ~T~ ~(T ≤ 5)~, là số lượng bộ test.
• Dòng đầu tiên của mỗi bộ test là ~N~, số lượng ngọn núi.
• Dòng thứ hai của mỗi bộ test gồm ~N~ số nguyên dương ~h_1, h_2, …, h_N~ ~(h_i ≤ 10^9)~ là độ cao của các ngọn núi.

OUTPUT

• Gồm ~T~ dòng, mỗi dòng là tổng năng lượng nhỏ nhất tương ứng với mỗi bộ test

Ví dụ

Input

3
5
2 4 3 2 5
10
6 9 9 6 6 4 4 4 4 4
2
18 5

Output

3
6
0

Giải thích:

• Ở bộ test 1, ta chọn ~K = 4~ và đặt 2 thiết bị thu sóng ở vị trí ~3~ và ~5~. Khi đó tổng năng lượng cần dùng sẽ là ~ |2 - 3| + |4 - 3| + |3 - 3| + |2 - 3| + |5 - 5| = 3 ~.
• Ở bộ test 1, ta có thể chọn ~K = 3~ và 2 thiết bị thu sóng ở vị trí ~2~ và ~4~. Khi đó tổng năng lượng cần dùng sẽ là ~ |2 - 4| + |4 - 4| + |3 - 4| + |2 - 5| + |5 - 5| = 6 ~, nhưng đây sẽ không phải là đáp án tối ưu.

Subtask 1: ~30~% số test thỏa mãn ~N ≤ 100~

Subtask 2: ~30~% số test thỏa mãn ~N ≤ 1000~

Subtask 3: ~40~% số test thỏa mãn ~N ≤ 100000~

Thành phố NQ là thành phố có tiềm năng về ngành du lịch vô cùng to lớn với nhiều danh lam thắng cảnh độc đáo. Tuy nhiên, chính quyền trước đây vẫn chưa thật sự quan tâm và khai phá hết những tiềm năng này. Thế nhưng trong những năm gần đây, tình hình đã dần được thay đổi với rất nhiều dự án và sự đầu tư mạnh tay vào lĩnh vực du lịch của nhiều tổ chức. Và một trong những thay đổi đó chính là việc quy hoạch lại các tuyến đường giao thông. Có ~N~ danh lam thắng cảnh ở thành phố NQ. Chính quyền dự tính sẽ xây dựng ~N - 1~ tuyến đường hai chiều, mỗi tuyến đường nối trực tiếp 2 danh lam thắng cảnh với nhau sao cho luôn tồn tại đường đi (trực tiếp hoặc gián tiếp) giữa 2 danh lam thắng cảnh bất kỳ. Mỗi danh lam thắng cảnh sẽ có một độ thu hút khách du lịch riêng, danh lam thứ i sẽ có sức thu hút ~a_i~. Một tour du lịch sẽ bắt đầu từ danh lam thứ ~u~ và kết thúc ở danh lam thứ ~v~ ~(u < v)~ sao cho mỗi danh lam được thăm tối đa 1 lần và sẽ có sức thu hút là sức thu hút của danh lam có sức thu hút lớn nhất trên đường đi đó. Nhiệm vụ của bạn là tính tổng sức thu hút của tất cả các tour du lịch.

INPUT

• Dòng đầu tiên là số nguyên dương N ~(N \geq 2)~, là số danh lam thắng cảnh của thành phố NQ.
• Dòng tiếp theo là gồm ~N~ số nguyên dương ~a_1, a_2, ... , a_N (a_i ≤ 10^6)~ là sức thu hút của các thành phố.
• ~N - 1~ dòng tiếp theo, gồm 2 số nguyên dương ~u~ và ~v~, cho biết có 1 đường đi 2 chiều nối trực tiếp 2 thành phố thứ ~u~ và ~v~

OUTPUT

• Gồm 1 số nguyên duy nhất là tổng sức thu hút của tất cả các tour du lịch.

Ví dụ

Input 1

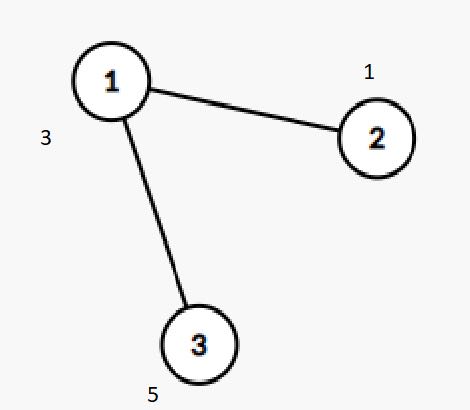
3
3 1 5
1 2
1 3

Output 1

13

Input 2

9
6 3 2 8 10 5 1 7 4
1 3
2 3
3 4
3 6
4 5
6 7
7 8
7 9

Output 2

255

Subtask 1: ~25~% số test thỏa ~N ≤ 300~

Subtask 2: ~25~% số test thỏa ~N ≤ 3000~

Subtask 3: ~25~% số test thỏa ~N ≤ 300000~, đường đi giữa 2 danh lam bất kỳ có độ dài bé hơn ~3~

Subtask 4: ~25~% số test thỏa ~N ≤ 300000~

Giải thích test 1

• Tour du lịch từ danh lam thứ ~1~ tới danh lam thứ ~2~ có sức hút là ~3~.
• Tour du lịch từ danh lam thứ ~1~ tới danh lam thứ ~3~ có sức hút là ~5~.
• Tour du lịch từ danh lam thứ ~2~ tới danh lam thứ ~3~ có sức hút là ~5~.
• Tổng sức hút của tất cả các tour du lịch là ~3 + 5 + 5 = 13~.