Thi thử HSG 11 - Round 2 (by steveonalex and swishy)
Points: 5
Sửu có một xâu nhị phân ~S~ độ dài ~N~. Trong một thao tác, Sửu có thể chọn một vị trí ~i~ ~(1 \leq i \leq N - 1)~ sao cho ~S_i~ ~\neq~ ~S_{i+1}~ và đổi chổ ~S_i~ và ~S_{i + 1}~ cho nhau. Nói cách khác, Sửu có thể dịch chuyển một kí tự 1 qua lại trong một thao tác.
Ví dụ: Cho xâu 1101010. Sửu có thể chọn ~i = 3~ để nhận được xâu mới là 1110010, hay ~i = 4~ để nhận được xâu mới là 1100110.
Gọi độ đẹp của xâu ~S~ là độ dài của xâu con dài nhất chỉ chứa kí tự 1.
Ví dụ: Độ đẹp của xâu 1101010 là ~2~.
Gọi ~G(S)~ là độ đẹp lớn nhất của xâu ~S~ sau khi thực hiện không quá ~K~ thao tác. Để tăng thử thách cho mình, Sửu đặt thêm ~Q~ câu hỏi. Ở câu hỏi thứ ~i~, Sửu sẽ đảo ngược đoạn ~[l, r]~ ~(1 \leq l \leq r \leq N)~ của xâu ~S~ (Chuyển kí tự 1 thành 0 hoặc ngược lại).
Gọi ~S_i~ là xâu ~S~ sau câu hỏi thứ ~i~, với mỗi câu hỏi, bạn hãy giúp Sửu tính ~G(S_i)~.
Input
- Dòng đầu tiên nhập ba số ~N~, ~K~ và ~Q~ ~(N \leq 10^6, K \leq 10^9, Q \leq 50)~ lần lượt là độ dài của xâu ~S~, số thao tác tối đa và số câu hỏi mà Sửu đặt ra.
- Dòng thứ hai nhập vào xâu ~S~.
- ~Q~ dòng sau, dòng thứ ~i + 2~ nhập vào hai số ~l~ và ~r~ ~(1 \leq l \leq r \leq N)~ thể hiện cho câu hỏi thứ ~i~.
Output
- Gồm ~Q + 1~ dòng, dòng thứ ~i~ thể hiện cho ~G(S_i)~.
Sample Input
5 2 3
10101
3 3
2 4
1 5
Sample Output
3
1
5
0
Giải thích test mẫu:
- ~S~ ban đầu là
10101, ta có thể chọn ~i = 1~, sau đó chọn ~i = 4~ để nhận được xâu01110có độ đẹp là ~3~ trong ~2~ thao tác, đây cũng là độ đẹp lớn nhất có thể. - Sau câu hỏi thứ ~1~, ~S~ trở thành
10001có độ đẹp là ~1~, có thể chứng minh được ta không thể tăng độ đẹp trong không quá ~2~ thao tác. - Sau câu hỏi thứ ~2~, ~S~ trở thành
11111có độ đẹp là ~5~, vì ta không thể thực hiện thêm thao tác nên đây là độ đẹp lớn nhất có thể. - Sau câu hỏi thứ ~3~, ~S~ trở thành
00000có độ đẹp là ~0~, vì ta không thể thực hiện thêm thao tác nên đây là độ đẹp lớn nhất có thể.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~25 \%~ | ~N \leq 500~ |
| ~2~ | ~25 \%~ | ~K \leq 1~ |
| ~3~ | ~25 \%~ | ~Q = 5~ |
| ~4~ | ~25 \%~ | Không ràng buộc gì thêm |
Points: 5
Tí có một đồ thị vô hướng gồm ~N~ đỉnh và ~M~ cạnh (có thể không liên thông). Tí đang rất hạnh phúc với đồ thị của mình, nhưng mọi việc không đơn giản như thế. Tí đột nhiên nhận ra đồ thị của mình là không ổn định.
Sau một hồi tính toán, Tí thấy rằng đồ thị của mình phải thỏa mãn ~Q~ yêu cầu, mỗi yêu cầu được biểu diễn bằng một cặp số ~(u, v)~, nghĩa là phải tồn tại đường đi giữa hai đỉnh ~(u, v)~ trên đồ thị của Tí. Chỉ khi thỏa mãn tất cả ~Q~ yêu cầu, đồ thị của Tí mới được xem là ổn định.
Tuy nhiên, trong xã hội này, cần cù thì bù siêng năng, chỉ có làm mới có ăn. Để có thể thêm một cạnh ~(u, v)~ vào đồ thị, Tí phải tốn một chi phí là ~u \times v~. Vì Tí là sinh viên cuối tháng (Tí cũng muốn có ăn), nên anh ấy muốn tìm một cách nối để đồ thị của anh ấy là ổn định, sao cho tổng chi phí nối là thấp nhất có thể. Các bạn hãy giúp Tí nhé.
Input
- Dòng đầu tiên nhập vào ba số ~N, M, Q~ ~(1 \leq N, M, Q \leq 2 \times 10^5)~ lần lượt là số đỉnh, số cạnh của đồ thị và số yêu cầu.
- ~M~ dòng tiếp theo, mỗi dòng nhập vào hai số ~u~ và ~v~ ~(1 \leq u, v \leq N)~ thể hiện cho cạnh nối giữa hai đỉnh ~u~ và ~v~.
- ~Q~ dòng cuối cùng, dòng thứ ~j~ nhập vào hai số ~a~ và ~b~ ~(1 \leq a, b \leq N)~ thể hiện cho yêu cầu thứ ~j~.
Output
- In ra kết quả của bài toán trên.
Sample Input
7 4 3
1 2
3 4
5 6
6 7
1 4
4 7
3 5
Sample Output
8
Giải thích test mẫu
Đồ thị trước khi thêm đỉnh
Đồ thị sau khi thêm đỉnh
- Tổng chi phí sau khi thêm đỉnh ~(1, 3)~ và ~(1, 5)~ là ~1 \times 3 + 1 \times 5 = 8~. Đây cũng là chi phí thấp nhất có thể.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~30 \%~ | ~N,M,Q \leq 10~ |
| ~2~ | ~30 \%~ | ~N,M,Q \leq 10^3~ |
| ~3~ | ~40 \%~ | Không ràng buộc gì thêm |
Points: 5
Dần là một học sinh lớp 10 rất giỏi toán. Trong một tiết toán nọ, Dần được thầy giáo giao cho một bài tập:
Cho một số ~n~, tính ~2^{C_n^0} \times 2^{C_n^1} \times 2^{C_n^2} \times … \times 2^{C_n^n}~.
Dĩ nhiên, đây là một bài toán rất dễ, và Dần đã giải được nó ngay lập tức. Thầy giáo đành phải đưa ra một bài toán khó hơn chút:
Cho hai số ~n~ và ~x~, tính ~x^{C_n^0} + x^{C_n^1} + x^{C_n^2} + … + x^{C_n^n}~ (thay vì nhân thì sẽ là cộng).
Tưởng ngon ăn, Dần xung phong lên bảng làm bài. Đáng tiếc thay, sau cả buổi loay hoay, Dần vẫn chưa thể nào tính được. Các bạn hãy giúp Dần nhé.
Input
- Đọc vào hai số ~n~ và ~x~ ~(1 \leq n \leq 5 \times 10^5, 1 \leq x < 10^9+7)~
Output
- In ra ~n + 1~ số, số thứ ~i~ là ~\sum_{j=0}^{i}x^{C_n^j}~. Vì kết quả có thể rất lớn, bạn cần in kết quả modulo cho ~10^9+7~.
Sample Input
5 2
Sample Output
2 34 1058 2082 2114 2116
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~30 \%~ | ~N \leq 60~ |
| ~2~ | ~30 \%~ | ~N \leq 5000~ |
| ~3~ | ~40 \%~ | Không ràng buộc gì thêm |
Points: 5
Cho bàn bi băng có kích cỡ ~N * M~ đơn vị, ta quy ước các hàng được đánh số từ trái sang phải, các cột được đánh số từ trên xuống dưới. Ô ~(x, y)~ là giao của hàng ~x~ và cột ~y~.
Có ~Q~ truy vấn, mỗi truy vấn có dạng ~(x,y,\alpha,k)~, tức là giả sử bạn đặt bi cái ở ô ~(x, y)~, căn một góc ~\alpha~ và bắn bi với một lực sao cho bi cái sẽ di chuyển đúng ~\sqrt2 \times k~ đơn vị. Hỏi bi cái sẽ đập băng bao nhiêu lần (nếu ta giả sử rằng không có lực ma sát giữa mặt bàn và bi cái và bi cái sẽ lập tức dừng lại sau khi đi đúng ~k~ đơn vị). Nếu bi cái chạm vào góc và bật lại, ta coi như bi cái chỉ đập băng ~1~ lần.
Bởi vì đề ban đầu quá dễ, nên ~\alpha~ sẽ được giới hạn bởi các góc chéo (góc ~45^{\circ}, 135^{\circ}, 225^{\circ}, 315^{\circ}~).
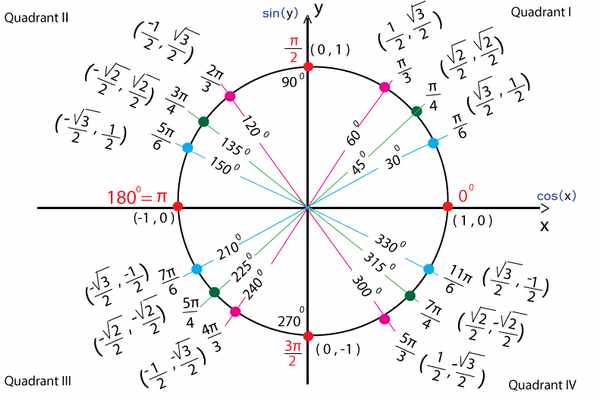
Các góc ở đây được hiểu theo nghĩa là góc lượng giác. Bạn có thể xem kỹ hơn về bảng giá trị góc lượng giác trong hình dưới đây.
Input
- Dòng đầu tiên nhập hai số ~N~, ~M~ ~(3 \leq N, M \leq 10^9)~ là số hàng và số cột của bàn bi.
- Dòng thứ hai nhập vào một số ~Q~ ~(1 \leq Q \leq 10^5)~ là số truy vấn.
- ~Q~ dòng sau, mỗi dòng nhập vào bốn số ~x, y, \alpha, k~ ~(1 \leq x \leq N, 1 \leq y \leq M, \alpha \in \left \{ 45, 135, 225, 315 \right \}, 1 \leq k \leq 10^{18})~ lần lượt là vị trí xuất phát, góc bắn và quãng đường mà bi cái sẽ di chuyển.
Output
- Gồm ~Q~ dòng, dòng thứ ~i~ thể hiện cho truy vấn thứ ~i~.
Sample Input
3 4
2
2 2 315 4
2 3 315 4
Sample Output
3
2
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~25 \%~ | ~N,M \leq 100, k \leq 10^4, Q \leq 10^3~ |
| ~2~ | ~25 \%~ | ~N,M \leq 10^5, Q \leq 10~ |
| ~3~ | ~25 \%~ | ~N,M \leq 10^5~ |
| ~4~ | ~25 \%~ | Không ràng buộc gì thêm |

