Giáo sư Nghĩa là nhà nghiên cứu về sinh vật học. Khi nghiên cứu về gen di truyền của các cá thể động vật, mỗi đoạn thông tin về gen của mỗi cá thể được giáo sư ký hiệu bằng một xâu các ký tự liền nhau gồm các chữ cái in thường từ a đến z trong bảng chữ cái tiếng Anh. Hiện tại ông đang nghiên cứu một nhóm động vật có n cá thể, đoạn thông tin gen của các cá thể lần lượt là các xâu $S_1$,$S_2$,$S_3$,…,$S_n$, độ dài của mỗi xâu là số ký tự trong xâu. Vì một số đoạn thông tin gen có độ dài rất lớn, gây khó khăn cho việc nghiên cứu nên giáo sư quyết định cắt bỏ một số các ký tự cuối của mỗi đoạn (có thể có một đoạn nào đó không bị cắt) sao cho đoạn dài nhất chỉ còn k ký tự nhưng vẫn đảm bảo không có hai đoạn thông tin gen bất kỳ nào giống nhau.

Yêu cầu: Cho n đoạn thông tin gen đôi một khác nhau $S_1$,$S_2$,…,$S_n$ (n ≤ ${10}^5$), độ dài mỗi đoạn lớn hơn hoặc bằng 1, tổng độ dài tất cả các đoạn không vượt quá ${10}^6$. Các bạn học sinh giỏi môn Tin học hãy giúp giáo sư Nghĩa tìm giá trị k nhỏ nhất thỏa mãn yêu cầu trên.

Dữ liệu vào:

• Dòng đầu chứa số nguyên dương $n$;
• $n$ dòng tiếp theo, dòng thứ $i$ (1 ≤ $i$ ≤ $n$) chứa xâu gồm các chữ cái latin in thường biểu diễn đoạn gen $S_i$.

Hai số liên tiếp trên cùng dòng được ghi cách nhau bởi dấu cách.

Kết quả: Ghi ra một số nguyên là giá trị k nhỏ nhất tìm được.

Ví dụ:

INPUT

4
atgxatxgatgx
atgxatat
atgxx
atxgtaaxagttxxgt

OUTPUT

7

*Giải thích: *

Với k=7, ta có các đoạn: "atgxatx", "atgxata", "atgxx", "atxgtaa" đôi một khác nhau.

Ràng buộc:

• Có 30% số test tương ứng 30% số điểm có n ≤ 50,|$S_i$|≤100;
• Có 30% số test khác tương ứng 30% số điểm có 50 < n ≤ 1000,|$S_i$|≤1000;
• 40% số test còn lại tương ứng 40% số điểm có 1000 < n ≤${10}^5$.

Toán học luôn mang đến cho người nghiên cứu về nó nhiều điều thú vị, đặc biệt là những dãy số có quy luật. Ví dụ dãy số Fibonacci xuất phát từ bài toán cổ về sự sinh sản của loài thỏ hay dãy số Catalan trong đó số thứ n chính là số cách đặt n cặp dấu ngoặc mở và đóng sao cho đúng quy tắc ưu tiên tính toán trong biểu thức toán học. Số Catalan thứ n cũng là đáp án của bài toán đếm số cách chia đa giác lồi có n+2 đỉnh thành các tam giác bằng cách vẽ các đường chéo sao cho chúng không cắt nhau trong đa giác.

Tèo rất thích nghiên cứu về các quy luật của dãy số, một hôm anh ấy phát hiện ra dãy số 0, 1, 3, 4, 9, 10,… có quy luật: Nếu gọi hai số đầu tiên của dãy là $a_0$ = 0 và $a_1$ = 1 thì $a_n$ (n = 2, 3, 4,…) là số tự nhiên nhỏ nhất không tạo thành một cấp số cộng với bất kỳ hai số nào đứng trước nó trong dãy số.

Yêu cầu: Cho trước số nguyên n, bạn hãy tìm số $a_n$ trong dãy số với quy luật như trên.

Dữ liệu vào: Một số nguyên dương n.

Kết quả: Ghi ra số nguyên $a_n$ tìm được.

Ví dụ:

INPUT

7

OUTPUT

13

Giới hạn:

• Có 40% số test với 2 ≤ n ≤ 200.
• Có 30% số test với 200 < n ≤ 2000.
• Có 30% số test với 2000 < n ≤ ${10}^9$.

Tom sống ở thành phố XYZ, hàng ngày Tom thường chọn đường đi ngắn nhất từ nhà tới trường và từ trường về nhà. Thành phố XYZ mà Tom ở có n nút giao thông được đánh số từ 1 đến n. Nhà Tom nằm ở nút giao thông 1 còn trường học của Tom nằm ở nút giao thông n. Từ nút giao thông i đến nút j có không quá một đường đi một chiều độ dài $d_{ij}$, tất nhiên, có thể có đường đi một chiều khác đi từ nút j đến nút i. Trong thời gian tới, thành phố sẽ tổ chức nhiều sự kiện văn hóa và

Tom biết rằng, khi đi làm từ nhà đến cơ quan thì có p nút sẽ bị ùn tắc là $a_1$,$a_2$,..,$a_p$, còn khi đi từ trường về nhà thì có q nút sẽ bị ùn tắc là $b_1$,$b_2$,..,$b_q$. Tom băn khoăn muốn biết độ dài đường ngắn nhất đi từ nhà đến trường mà không đi qua các nút $a_1$,$a_2$,..,$a_p$ và độ dài đường ngắn nhất đi từ trường về nhà mà không đi qua các nút $b_1$,$b_2$,..,$b_q$ là bao nhiêu?

Ví dụ, thành phố có 5 nút giao thông và các đường đi một chiều với độ dài tương ứng như hình bên. Giả sử nút 4 là nút bị ùn tắc khi đi từ nhà đến trường, nút 2 và nút 4 là nút bị ùn tắc khi đi từ trường về nhà, khi đó độ dài đường đi ngắn nhất từ nhà đến trường là 19 (đường đi 1->2->3->5, không đi qua nút 4), độ dài đường đi ngắn nhất từ trường về nhà là 17 (đường đi 5->3->1, không đi qua nút 2 và nút 4)

Yêu cầu: Cho biết các đường đi một chiều với độ dài tương ứng mô tả hệ thống giao thông thành phố XYZ và các nút sẽ bị ùn tắc $a_1$,$a_2$,..,$a_p$, $b_1$,$b_2$,..,$b_q$. Hãy tìm độ dài đường đường đi ngắn nhất để đi từ nhà (nút giao thông 1) đến trường (nút giao thông n) mà không đi qua các nút $a_1$,$a_2$,..,$a_p$ và từ trường về nhà mà không qua các nút $b_1$,$b_2$,..,$b_q$.

Dữ liệu vào:

• Dòng đầu ghi bốn số nguyên dương $n,m,p,q$ (3 ≤ $n$ ≤ 10000, $m$ ≤ ${10}^5$, 1 ≤ $p,q$ ≤ $n-2$)
• Dòng thứ hai ghi $p$ số nguyên $a_1$,$a_2$,..,$a_p$ (1 < $a_i$ < $n$)
• Dòng thứ ba ghi $q$ số nguyên $b_1$,$b_2$,..,$b_q$ (1 < $b_i$ < $n$)
• m dòng tiếp theo, mỗi dòng 3 số nguyên $i,j$, $d_{ij}$ (1 ≤ $i,j$ ≤ $n$, 0 < $d_{ij}$ ≤ 30000) mô tả có đường đi một chiều từ i đến j có độ dài $d_{ij}$.

Hai số liên tiếp trên một dòng cách nhau một dấu cách. Dữ liệu bảo đảm luôn có nghiệm.

Kết quả: Gồm một dòng chứa 2 số nguyên cách nhau một dấu cách, số thứ nhất là độ dài đường đi ngắn nhất từ nhà đến trường, số thứ hai là độ dài ngắn nhất từ trường về nhà thỏa mãn điều kiện đã nêu.

Ví dụ:

INPUT:

5 11 1 2
4
2 4
1 2 10
1 4 3
2 3 6
2 5 10
3 1 12
3 4 6
3 5 3
4 1 5
4 3 5
5 3 5
5 4 10

OUTPUT

19 17

Chú ý: 50% số test có n≤100

Tại TP, có tất cả n thượng nghị sĩ ở trong n ngôi nhà (đánh số từ 1 đến n), giữa hai ngôi nhà có một đường đi duy nhất: đường đi trực tiếp hoặc không trực tiếp (đi qua các con đường khác). Tất cả các ngôi nhà đều đi được đến nhau.

Mỗi thượng nghị sĩ khi đi từ nhà mình đến thượng viện, phải trả 1 USD khi đi qua một con phố (con phố là đường nối trực tiếp hai ngôi nhà bất kỳ). Người đứng đầu thượng viện đã nghĩ cách làm sao cho số tiền mà các thượng nghị sĩ phải trả là tối thiểu.

Vì vậy, ông ra quyết định:

• Có k con phố miễn phí (thượng nghị sĩ sẽ không phải trả tiền khi đi trên con phố này).
• Đặt tòa nhà thượng viện ở một trong n ngôi nhà.

Yêu cầu: Hãy viết chương trình tính xem chi phí tối thiểu là bao nhiêu? Dữ liệu vào:

• Dòng 1: Số nguyên n và k tương ứng là số ngôi nhà ở TP và số con phố miễn phí.
• n – 1 dòng tiếp theo, mỗi dòng chứa 2 số i, j có nghĩa là có con phố nối ngôi nhà i và ngôi nhà j. (1< n ≤ 10000; 0 < k < n ; 1≤ i, j ≤ n ; i ≠ j)

Kết quả: Một số duy nhất là chi phí tối thiểu phải trả.

Ví dụ:

INPUT:

13 3
1 2
2 3
2 8
7 8
7 5
5 4
5 6
8 9
8 10
10 11
10 12
10 13

OUTPUT:

11

Giải thích:

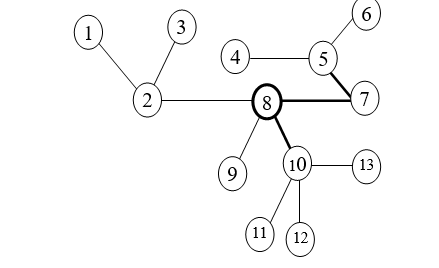
Phương án giải quyết: 5 - 7, 7 - 8, 8 - 10 là những con phố miễn phí và 8 là thượng viện. Chi phí tối thiểu là: 11.

Ràng buộc:

• Có 30% số test ứng với 30% số điểm của bài có n ≤ 30
• Có 40% số test ứng với 40% số điểm của bài có 30 < n ≤ 5000
• Có 30% số test ứng với 30% số điểm của bài có 5000 < n ≤ 10000.