Bob152 từ bé đã luôn mong ước có thể giúp gì đó vào việc giảm thiểu khả năng tai nạn khi đi xe và an toàn giao thông. Bây giờ khi đã lớn khôn và thành sugar daddy của chính mình (Depressed Bob) , Bob152 đã có cơ hội để thực hiện ước mơ của mình.Với mối quan hệ rộng , anh ta có thể thuê kĩ sư xây dựng lại T tuyến đường (T ~\leq~ 1000) .Mỗi tuyến đường có n đỉnh và m con đường 2 chiều nối hai đỉnh khác nhau với nhau đảm bảo từ 1 đỉnh bất kỳ có thể đi đến tất cả các đỉnh còn lại.Mỗi con đường có tốc độ tối đa là w (~w_i \leq 10^9~) mà người dân phải tuân thủ theo . Bob152 muốn đập bớt đi m – n+1 con đường sao cho các con đường còn lại phải được nối với nhau và từ 1 đỉnh có thể đi đến tất cả các đỉnh còn lại.Anh ta chọn ra 1 số k (~k \leq 10^9~) .Bob152 tin rằng nếu mọi con đường còn lại sau khi đập bớt m-n+1 con đường sẽ ít xảy ra tai nạn hơn nếu con đường có tốc độ tối đa lớn nhất sau khi đập m-n +1 con đường đúng bằng k.Bob152 có thể tùy ý thay đổi tốc độ tối đa của mỗi con đường giảm 1 hoặc tăng 1 đơn vị , khi đó Bob152 tốn 1 đô tiền mua chuộc công nhân xây dựng. Bob152 không muốn tốn quá nhiều tiền cũng như tiết kiệm ngân sách nhà mình để mua PC 500 củ nên bạn hãy giúp Bob152 tính toán số tiền nhỏ nhất cần phải bỏ ra để hoàn thành tâm nguyện của anh ấy.

Input :

Dòng đầu tiên chứa T (T <= 1000) tuyến đường.

Trong dòng đầu tiên của mỗi tuyến đường cần xét tiếp theo là 3 số n , m và k ( ~2 \leq n \leq~ ~2~ x ~10^5~ ; ~n-1 \leq m~ ~;\leq~ min(~2~ x ~10 ^5~ , ~n*(n-1)/2~ ) , ~1 \leq k \leq 10^9~.

Sau đó m dòng tiếp theo , dòng thứ i chứa ba số ui , vi và wi (~1 \leq u_i , v_i \leq n~ ; ~u_i != v_i~ ; ~1\leq w_i \leq 10^9~). Thể hiện rằng có cạnh nối từ đỉnh u tới đỉnh v và có tốc độ tối đa là wi.

Output :

In ra số tiền tối thiểu mà Bob152 phải trả để giảm thiểu tai nạn giao thông.

Example input :

4
4 5 7
4 1 3
1 2 5
2 3 8
2 4 1
3 4 4
4 6 5
1 2 1
1 3 1
1 4 2
2 4 1
4 3 1
3 2 1
3 2 10
1 2 8
1 3 10
5 5 15
1 2 17
3 1 15
2 3 10
1 4 14
2 5 8

Example output :

1
3
0
0

Subtask 1 : ~n \leq 10~ và ~T \leq 100~.

Subtask 2 : ~n \leq 20~ và ~T \leq 100~.

Subtask 3 : Tổng ~n~ các test ~\leq~ ~2~ x ~10^5~ và ~m~ = ~n~-1.

Subtask 4 : Tổng ~n~ các test ~\leq~ ~2~ x ~10^5~ và mọi con đường đều có chung 1 tốc độ tối đa.

Subtask 5 : Tổng ~n~ các test ~\leq~ ~2~ x ~10^5~ và không ràng buộc gì thêm.

Với mỗi subtask ta được 20% điểm của bài.

Giải thích test :

Testcase 1 : Đồ thị có dạng như thế này.

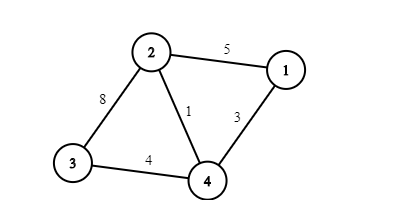
Ta bỏ đi cạnh (3 ,4) và (1 ,4 ).Thì ta được :

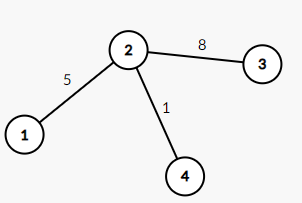
Ta thấy con đường 2 -> 3 có tốc độ tối đa lớn nhất là 8 nhưng lớn hơn k đề cho là 7. Nên ta chỉ cần giảm tốc độ tối đa của con đường này đi 1 đơn vị và tốn 1 đô.