ami có một cây ~n~ nút, mỗi đỉnh được đánh số từ ~1~ đến ~n~, nút ~i~ được gắn số ~a_i~. Một đường đi từ ~u~ đến ~v~ là đường đi xuất phát từ ~u~, đi qua các đỉnh kề không quá một lần và kết thúc ở ~v~. Các bạn cần tính xem có bao nhiêu giá trị ~D \geq 0~ mà tồn tại ít nhất một đường đi giữa 2 nút trên cây là một cấp số cộng công sai ~D~. Với mỗi ~D~ tìm được, hãy tìm ra đường đi có độ dài lớn nhất thoả mãn điều kiện. Độ dài đường đi giữa 2 nút ~u~ và ~v~ là số lượng nút nằm trên đường đi đó.

Input

Dòng đầu tiên gồm một số nguyên dương ~n~ là số đỉnh của cây.

~n-1~ dòng tiếp theo, mỗi dòng chứa 2 số ~u~ và ~v~ biểu diễn một cạnh nối giữa 2 đỉnh ~u~ và ~v~.

Dòng tiếp theo gồm ~n~ số nguyên ~a_1~, ~a_2~, ~a_3~, ..., ~a_n~. ~A_i~ là giá trị trên nút ~i~

Output

Gồm một vài dòng, mỗi dòng có 2 số ~D~ ~x~. Với ý nghĩa, đường đi dài nhất có công sai ~D~ có độ dài là ~x~.

Các bạn cần in D theo thứ tự tăng dần.

Sample Input 1

9
1 2
1 3
2 4
2 5
3 6
3 7
5 8
7 9
1 4 0 3 7 -1 -1 10 -2

Sample Output 1 ##

1 4
3 4

Giải thích

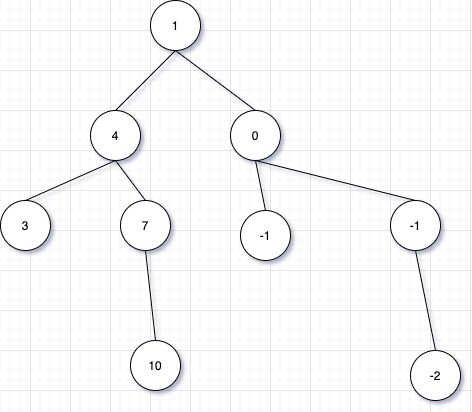
Một đường đi có công sai 1 là đường đi từ nút 9 đến 1. Dãy số là -2 -1 0 1 và có độ dài là 4

Một đường đi có công sai 3 là đường đi từ nút 1 đến nút 8. Dãy số là 1 4 7 10 và có độ dài là 4.

Giới hạn

~2 \leq n \leq 3*10^5~.

~1? \leq a_i \leq 10^9~.