Cho một lưới chữ nhật gồm ~N~ dòng và ~M~ cột, các dòng được đánh số từ ~1~ đến ~N~ từ trên xuống dưới, các cột được đánh số từ ~1~ đến ~M~ theo thứ tự từ trái sang phải. Mỗi ô sẽ được tô một màu xanh hoặc trắng. Nếu ~S_{x,y} =1~, ô nằm ở dòng ~x~ và cột ~y~ có màu xanh; nếu ~S_{x,y} =0~ thì ô đó có màu trắng.

Từ một ô bất kì, có thể di chuyển sang một ô khác kề với nó (có chung cạnh) và có cùng màu với nó. Nói cách khác, từ một ô ~(x,y)~, ta có thể di chuyển sang ô ~(x′,y′)~ khi và chỉ khi các điều kiện sau được thỏa mãn:

• ~|x−x′|+|y−y′|=1~
• ~S_{x,y} = S_{x′,y′}~

Lưới chữ nhật đã cho có tính chất đặc biệt sau: với cặp ô xanh ~a~ và ~b~ bất kì, có tối đa một đường đi đơn (đường đi chỉ đi qua mỗi ô tối đa một lần) xuất phát từ ~a~ và kết thúc tại ~b~.

Có ~Q~ truy vấn, mỗi truy vấn được mô tả bởi bốn số nguyên ~x_1, y_1, x_2, y_2~, yêu cầu:

• Xét lưới chữ nhật con gồm các ô từ dòng ~x_1~ đến dòng ~x_2~, từ cột ~y_1~ đến cột ~y_2~. Cho biết có bao nhiêu thành phần liên thông gồm các ô màu xanh trong lưới chữ nhật con này.

Hãy viết chương trình xử lí ~Q~ truy vấn trên.

Dữ liệu

• Dòng đầu tiên gồm ba số nguyên ~N,M,Q~ ~(1≤N,M≤2000,1≤Q≤200000)~ - sốdòng, số cột của lưới chữ nhật và số truy vấn cần xử lý.
• ~N~ dòng tiếp theo, mỗi dòng gồm một xâu ~M~ kí tự, mỗi kí tự có giá trị ~0~ hoặc ~1~ - mô tả lưới chữ nhật. Dữ liệu vào đảm bảo có tối đa một đường đi đơn giữa hai ô màu xanh bất kì.
• ~Q~ dòng tiếp theo, mỗi dòng gồm bốn số nguyên ~x_1,y_1,x_2,y_2~ ~(1≤x_1 ≤x_2 ≤ N, 1≤y_1 ≤y_2 ≤ M)~ - mô tả một truy vấn.

Kết quả

• In ra ~Q~ số nguyên lần lượt là câu trả lời cho các truy vấn..

Ví dụ

Sample Input

4 5 5
10101
11101
00011
11100
2 2 3 4
3 1 4 3
2 3 4 5
3 1 3 3
1 1 4 5

Sample Output

2 
1
3
0
3

Giải thích

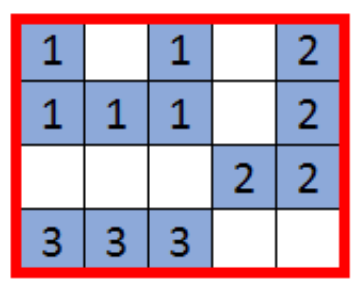
Hình vẽ minh họa cho các truy vấn:

• Truy vấn thứ nhất

  

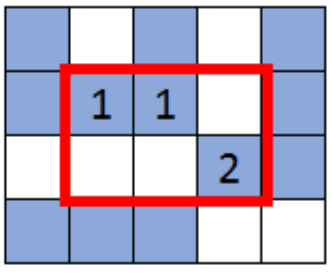
• Truy vấn thứ hai

  

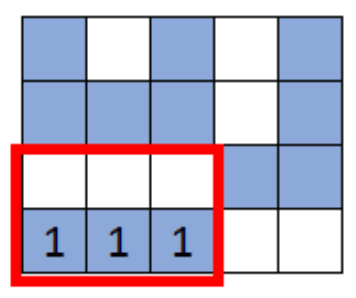
• Truy vấn thứ ba

  

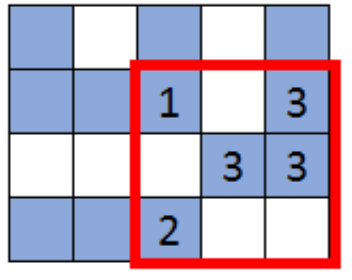
• Truy vấn thứ tư

  

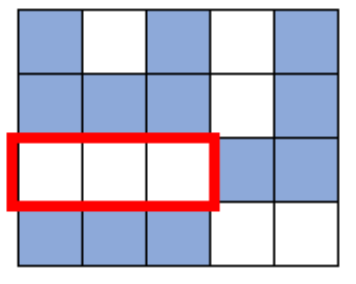
• Truy vấn thứ năm

  

Chấm điểm

• Subtask 1 (30% số điểm): ~N,M ≤ 50, Q ≤ 2000~
• Subtask 2 (70% số điểm): Không có ràng buộc gì thêm

Nguồn: Free Contest