Nguồn: Code Festival 2016 - Elimination Tournament Round 1 - Problem A

Trước hết, với phương án đặt trạm điện tại hai thành phố ~A~ và ~B~, ta có thể xem như chỉ đặt trạm điện tại thành phố ~A~, và có thể xây dựng đường dây điện nối giữa ~A~ và ~B~ với chi phí ~0~. Từ đó, ta nghĩ ra được thuật toán cho hai subtask đầu tiên: bổ sung thêm cạnh ~(A, B, 0)~ và tìm cây khung cực tiểu (minimum spanning tree) của đồ thị ~M + 1~ cạnh bằng thuật toán Kruskal. Thuật toán trên có độ phức tạp ~O(QM log(N + M))~.

Để cải tiến thuật toán trên, ta cần hiểu bản chất của thuật toán Kruskal. Trước hết, ta sẽ tìm cây khung cực tiểu ~T~ của đồ thị ~M~ cạnh. Nhận xét rằng, khi bổ sung một cạnh có trọng số ~0~ giữa hai đỉnh ~A~ và ~B~, cạnh này chắc chắn sẽ nằm trong cây khung tối thiểu. Khi đó, đường đi giữa ~A~ và ~B~ trong ~T~ và cạnh ~(A,B)~ sẽ tạo thành một chu trình. Do thuật toán Kruskal xét các cạnh theo trọng số từ nhỏ đến lớn, cạnh có trọng số lớn nhất trên đường đi giữa ~A~ và ~B~ sẽ bị bỏ ra khỏi cây khung cực tiểu.

Do đó, gọi ~W~ là tổng trọng số của các cạnh trong ~T, maxW(u,v)~ là cạnh có trọng số lớn nhất trên đường đi giữa ~u~ và ~v~ trên ~T~. Khi đó, với truy ván ~i~, đáp án sẽ là ~W − maxW(A_i,B_i)~.

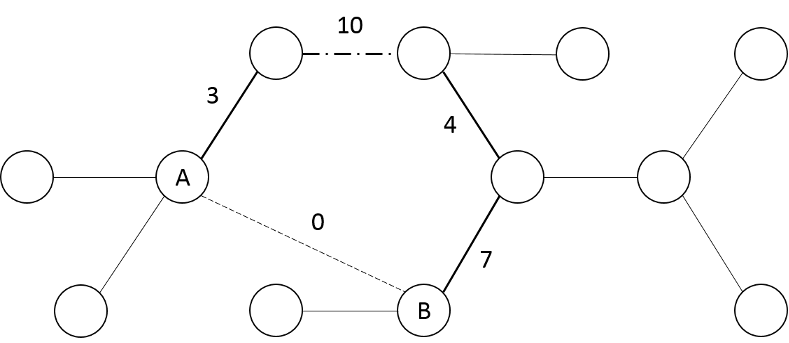
Đến đây, ta đã có lời giải độ phức tạp ~O(Mlog(N +M)+QN)~, đủ để vượt qua subtask 3. Để được trọn vẹn điểm bài này, ta cần thực hiện việc tính toán trước ~maxW(u,v)~ với mọi cặp ~(u,v)~ trong ~O(N^2)~ bằng cách DFS từ từng đỉnh. Khi đó, mỗi truy vấn có thể được trả lời trong ~O(1)~.

Độ phức tạp: ~O(Mlog(N+M)+N^2 +Q)~.