Một vùng biển được một tả bởi hệ trục tọa độ ~Oxy~. Có ~N ∗ M~ con cá hiện đang sinh sống trên vùng biển, con cá thứ ~(i,j)~ có tọa độ ~(X_i,Y_j)~ và có giá trị ~A_{i,j}~ (với ~1≤i≤N,1≤j≤M~).

Một ngư dân đang chuẩn bị đánh bắt cá trong vùng biển. Để thực hiện đánh bắt cá, người ngư dân sẽ giăng một tấm lưới hình chữ nhật có cạnh song song với các trục tọa độ (chú ý là diện tích của tấm lưới có thể bằng ~0~). Nếu gọi tọa độ góc trái dưới của tấm lưới là ~(x_1,y_1)~ và tọa độ góc phải trên là ~(x_2, y_2) (x_1 ≤ x_2, y_1 ≤ y_2)~ thì lợi nhuận của ngư dân sẽ bằng tổng giá trị những con cá nằm trong tấm lưới (kể cả cạnh tấm lưới) trừ đi diện tích của tấm lưới. Cụ thể hơn, lợi nhuận được tính bằng công thức sau:

$$\left(\sum_{\substack{X_i\in[x_1,x_2]\\ Y_j\in[y_1,y_2]}} A_{i,j}\right) - (x_2 - x_1) (y_2 - y_1)$$

Hãy tìm lợi nhuận tối đa mà người ngư dân đạt được.

Dữ liệu

• Dòng đầu tiên gồm hai số nguyên ~N~ và ~M~ ~(1 ≤ N, M ≤ 400)~.
• Dòng thứ hai gồm một dãy ~N~ số nguyên ~X_1, X_2, ..., X_N (|X_i| ≤ 10^7, X_{i−1} < X_i)~.
• Dòng thứ ba gồm một dãy ~M~ số nguyên ~Y_1, Y_2, ..., Y_M (|Y_i| ≤ 10^7, Y_{i−1} < Y_i)~.
• ~N~ dòng tiếp theo, dòng thứ ~i~ gồm ~M~ số nguyên ~A_{i,1}, A_{i,2}, ..., A_{i,M} (0 ≤ A_{i,j} ≤ 10^9)~.

Kết quả

• In ra lợi nhuận lớn nhất mà ngư dân đạt được.

Ví dụ

Sample Input 1

4 3 
1 4 5 7
2 3 6
3 5 3
1 2 3
4 7 2
2 0 6

Sample Output 1

18

Sample Input 2

2 3
1 8
-4 -3 -2 
1 2 3
8 9 10

Sample Output 2

27

Giải thích

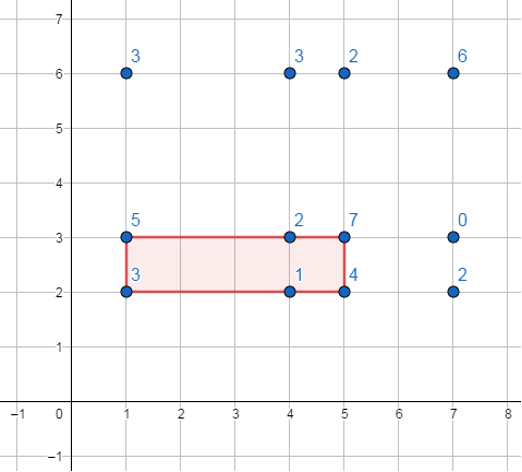
• Hình vẽ mô tả ví dụ thứ nhất (phần màu đỏ mô tả vị trí cần đặt của tấm lưới để đạt lợi nhuận lớn nhất). Lợi nhuận đạt được là: (3 + 5 + 1 + 2 + 4 + 7) − (5 − 1) ∗ (3 − 2) = 18.
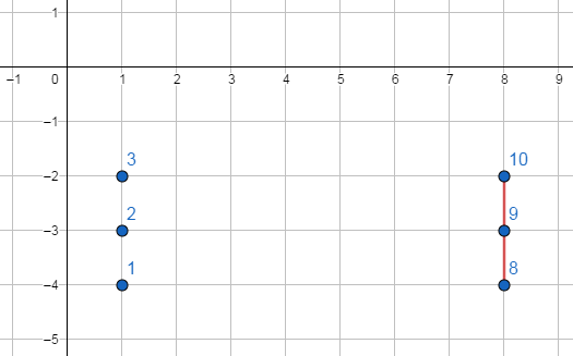
• Hình vẽ mô tả ví dụ thứ hai (diện tích tấm lưới trong trường hợp này bằng 0, được mô tả bằng đoạn thẳng màu đỏ). Lợi nhuận đạt được là: (8+9+10)−(8−8)∗(−2−(−4)) = 27.

Giới hạn

• Subtask 1 (15% số điểm): ~N, M ≤ 20~
• Subtask 2 (15% số điểm): ~N, M ≤ 40~
• Subtask 3 (20% số điểm): ~N, M ≤ 100~
• Subtask 4 (50% số điểm): Không có ràng buộc gì thêm

Nguồn: Free Contest