Phú Ông ngày xưa nổi tiếng là giàu có và lắm đất đai. Ông có một mảnh đất hình đa giác lồi gồm ~N~ đỉnh ~A_1,A_2,..,A_N~. Mảnh đất hình đa giác này được chia thành ~N – 2~ mảnh đất nhỏ hình tam giác bằng cách nối ~N – 3~ đường chéo giữa các cặp đỉnh. Các đường chéo chỉ có thể cắt nhau tại điểm mút. Nghĩa là hai mảnh đất bất kì hình tam giác này chỉ chung nhau nhiều nhất là một cạnh. Sau một thời gian dài làm việc chăm chỉ cho Phú Ông, Bờm được Phú Ông thưởng cho một số mảnh đất hình tam giác trong mảnh đất to hình đa giác lồi. Phú Ông yêu cầu Bờm chọn các mảnh đất hình tam giác sao cho không được chọn hai mảnh đất có chung cạnh. Bờm liền nghe lời và cố gắng chọn các mảnh đất sao cho tổng diện tích các mảnh đất được chọn là lớn nhất.

Yêu cầu: Tính xem, tổng diện tích của các mảnh đất mà Bờm chọn được có giá trị lớn nhất bằng bao nhiêu?

Dữ liệu gồm:

• Dòng đầu ghi số nguyên dương ~N~ là số đỉnh của đa giác lồi ~(4≤N)~.
• ~N~ dòng tiếp theo, mỗi dòng ghi hai số nguyên ~X_i,Y_i~ là tọa độ của điểm ~A_i, (|X_i |,|Y_i| ≤10^9)~.
• ~N – 3~ dòng tiếp theo, mỗi dòng ghi hai chỉ số ~i,j (1≤i≠j≤n)~ mô tả đường chéo nối hai đỉnh ~A_i~ và ~A_j~. Dữ liệu đảm bảo không có hai đường chéo nào cắt nhau ngoài các điểm mút của đường chéo.

Kết quả:

• Giá trị lớn nhất của tổng diện tích của các mảnh vườn hình tam giác mà Bờm có thể chọn được. Chú ý là nếu tổng diện tích có giá trị là số nguyên thì đưa ra số nguyên đó, nếu là số thập phân thì đưa ra giá trị có một chữ số thập phân.

Ví dụ:

Input

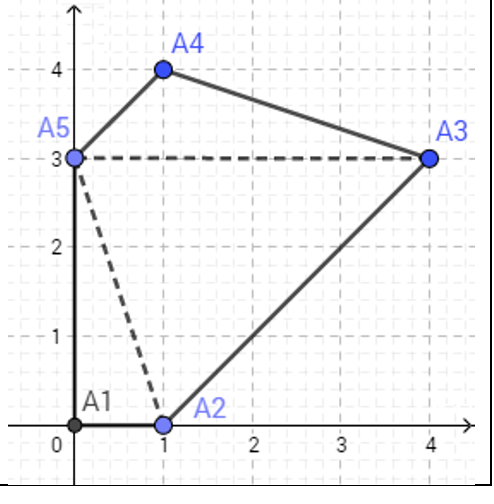
5
0 0
1 0
4 3
1 4
0 3
2 5
3 5

Output

6

Giải thích:

Bờm chọn mảnh đất tạo bởi tam giác ~A_2A_3A_5~.

Giới hạn:

• Có 20% số test ứng với ~4≤N ≤20~;
• Có 20% số test khác ứng với ~N ≤20000; N – 3~ đường chéo đều có cùng chung một điểm mút.
• Có 60% số test còn lại ứng với ~N ≤3000~;