Bảo Bay Bổng có một đồ thị dạng cây gồm ~n~ đỉnh và ~n − 1~ cạnh, đỉnh thứ ~i~ có trọng số là ~w_i~. Cậu nghĩ ra một thuật toán tính giá trị của cây như sau:

• Bước 1: Chọn ra ~1~ đường kính bất kì của cây (giả sử đường kính này có số đỉnh là ~d~), trong đó đường kính của cây là đường đi giữa hai đỉnh trong cây có khoảng cách lớn nhất.
• Bước 2: Chọn một trong hai đầu mút của đường kính này làm đỉnh xuất phát và đánh số thứ tự đặc biệt cho các đỉnh này lần lượt từ ~1~ tới ~d~ dọc theo đường kính (xem ví dụ để hiểu rõ hơn).

Khi đó, đặt ~x_i~ là số thứ tự đặc biệt được gán cho đỉnh có khoảng cách tới đỉnh ~i~ ngắn nhất trong số các đỉnh nằm trên đường kính được chọn. Ta nói giá trị của cây được tính bằng công thức:

$$S = \sum^{n}_{i=1}w_i.x_i$$

Trong tất cả các cách thực hiện thuật toán trên lên cây đã cho, đặt ~S_{max}~ là giá trị lớn nhất của cây có thể đạt được. Hãy giúp Bảo Bay Bổng tìm ra giá trị ~S_{max}~ này.

Dữ liệu

• Dòng đầu tiên chứa số nguyên dương ~n~ ~(2 ≤ n ≤ 10^6)~ — số đỉnh của cây.
• Dòng thứ hai chứa ~n~ số nguyên dương ~w_1,w_2,...,w_n (1 ≤ w_i ≤ 10^6)~ — trọng số của các đỉnh trên cây.
• ~n − 1~ dòng tiếp theo, mỗi dòng chứa hai số nguyên dương ~u,v~ ~(1 ≤ u,v ≤ n;u \neq v)~, biểu thị có một cạnh nối giữa đỉnh ~u~ và đỉnh ~v~. Dữ liệu bảo đảm tạo nên cấu trúc cây.

Kết quả

• In ra một số nguyên là kết quả của bài toán.

Ví dụ

Sample Input 1

6
1 2 3 4 5 6
1 2
2 3
2 4
5 6
4 5

Sample Output 1

73

Giải thích

Trong test ví dụ, ta lựa chọn ra đường kính gồm các đỉnh ~1,2,4,5,6~ và đánh số thứ tự lần lượt vào các đỉnh này.

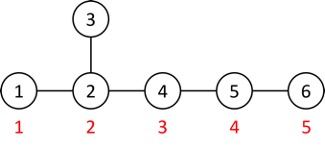
Giá trị của cây nếu ta thực hiện thuật toán như trên hình là: $$S = w_1 · 1 + w_2 · 2 + w_3 · 2 + w_4 · 3 + w_5 · 4 + w_6 · 5 = 73$$ Cũng với ví dụ đó, ta có thể sử dụng thuật toán trên theo một cách khác nhưng thu được kết quả không phải là giá trị lớn nhất:

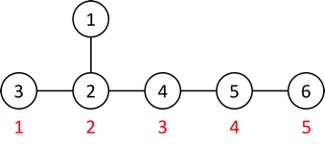
Giá trị của cây nếu ta thực hiện thuật toán như trên hình là: $$S = w_3 · 1 + w_2 · 2 + w_1 · 2 + w_4 · 3 + w_5 · 4 + w_6 · 5 = 71$$

Chấm điểm

• Subtask 1 (20% số test): ~n ≤ 100~
• Subtask 2 (30% số test): ~n ≤ 5000~
• Subtask 3 (50% số test): Không có ràng buộc gì thêm

Nguồn: Free Contest 124