Subtask 1

Duyệt trâu qua các đường kính trong ~O(n^2)~ và sử dụng các kĩ thuật, chẳng hạn như BFS multi source để tìm đỉnh trên đường kính được chọn có khoảng cách gần nhất đối với mỗi đỉnh trên cây, từ đó tính được giá trị của cây trong ~O(n)~

Độ phức tạp: ~O(n^3)~

Subtask 2

Cùng nhìn lại test ví dụ:

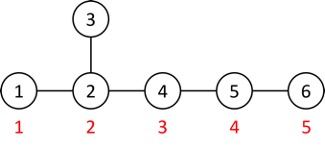
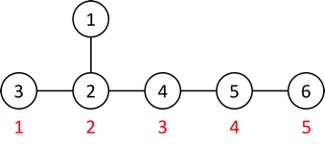
Hai cách điền số thứ tự vào cây có thể có rất nhiều điểm chung. Chẳng hạn với hai cách điền trên, giá trị của cây trong hai cách điền này đều có thành phần ~w_2 · 2 + w_4 · 3 + w_5 · 4 + w_6 · 5~. Do đó, ta có thể nghĩ ra một thuật toán tận dụng những điểm chung này: khi ta cố định gốc cây tại một đỉnh (chẳng hạn trong hai hình trên ta cố định gốc tại đỉnh ~6~), ta có thể quy hoạch động trên cây như sau: ~DP[i]~ là phần giá trị của cây nếu ta đánh số theo thứ tự từ gốc tới đỉnh ~i~. Như vậy ta có thể tính được giá trị của tất cả các cách điền vào đường kính có đầu mút tại gốc cây này trong ~O(n)~.

Độ phức tạp: ~O(n^2)~

Subtask 3

Ta có nhận xét như sau:

Trong một cây, nếu đường kính của cây có lẻ (hoặc chẵn) đỉnh thì các đường kính của cây sẽ có chung ~1~ (hoặc ~2~) điểm chính giữa.

Nhận xét này có thể dễ dàng chứng minh bằng phản chứng.

Sau đây sẽ là ý tưởng giải của trường hợp đường kính lẻ đỉnh, trường hợp chẵn có thể giải tương tự.

Ở đây nhắc lại một số định nghĩa được sử dụng trong đề bài:

• ~d~: số đỉnh của đường kính
• ~w_i~: trọng số của đỉnh thứ ~i~
• ~x_i~: số thứ tự đặc biệt được gán cho đỉnh có khoảng cách tới đỉnh ~i~ ngắn nhất trong số các đỉnh nằm trên đường kính được chọn. Lấy điểm chính giữa của đường kính làm gốc cây. Vì là điểm chính giữa của đường kính nên chắc chắn trong mọi cách điền số thứ tự, gốc này luôn mang số thứ tự ~\lceil\frac{d}{2} \rceil~, đặt số thứ tự này là ~mid~.

Ban đầu, ta coi như mọi đỉnh trong cây đều có giá trị ~x~ tương ứng của nó chính là ~mid~ và tổng giá trị của cây là:

$$S=\sum^{n}_{i=1}w_i.mid$$ Khi đó, ta phải chọn ra từ những đỉnh con trực tiếp của gốc này ~2~ nhánh có độ dài ~\lfloor\frac{d}{2} \rfloor~, một nhánh sẽ được gán số thứ tự ~1,2,...,mid−1~ và nhánh còn lại được gán số thứ tự ~mid+1,...,d~; những đỉnh bị ảnh hưởng bởi cách chọn này sẽ phải trừ đi từ mỗi đỉnh lượng giá trị là ~w_i · mid~

Ta sẽ giải quyết riêng biệt cách chọn của hai nhánh này. Nhận thấy là khi ta tách riêng biệt chúng ra, bài toán sẽ quay về chính subtask 2:

Cố định một gốc cây, với một cách điền số thứ tự vào, tính phần giá trị của cây thu được nếu đánh số theo thứ tự từ gốc cây đã chọn.

Ta có thể quy hoạch động trên cây cho từng bài toán con trong ~O(n)~ và sau đó tìm cách để chọn ra hai nhánh có thể kết hợp với nhau hợp lệ để tạo ra tổng lớn nhất trong ~O(n)~. Hai nhánh có thể kết hợp với nhau khi chúng có độ dài ~\lfloor\frac{d}{2} \rfloor~ và chúng xuất phát từ hai đỉnh con trực tiếp khác nhau của gốc.

Độ phức tạp: ~O(n)~